Weitzman's Pandora's Box Problem
Posted: 2018-07-20.
The "Pandora's Box" problem is a cool model of search for the best alternative under uncertainty with a neat and intuitive solution. This post describes a somewhat different proof and intuition with a nice extension to matching.
This proof is based on ideas in my 2016 paper with Bobby Kleinberg and Glen Weyl (which was inspired somewhat by Weber 1992), along with subsequent discussions.
Setup
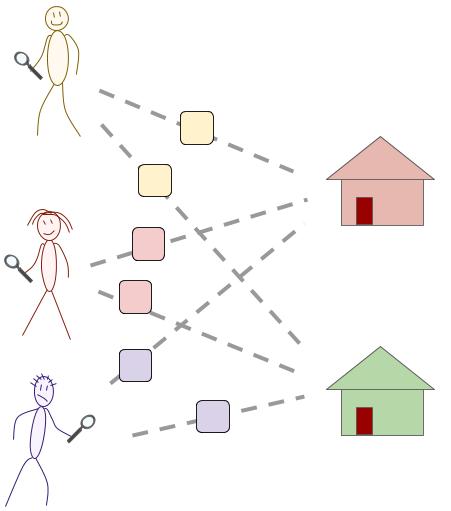
Picture, Weitzman (1979) says, a set of locked boxes with unknown contents. Box $i$ costs $c_i$ to open. But we have some information about the value $v_i$ of the prize inside; it is distributed according to $D_i$, independently of all other boxes' prizes. We can only carry home one of the prizes. So the problem is to decide which boxes to open, in what order, as well as when to stop opening and take home one of the prizes we've found.
The cost to open a box is $c_i$ and its value $v_i$ is drawn from $D_i$.
Weitzman named this problem "with apologies to connoisseurs of Greek Mythology". While I may not qualify as a connoisseur, I'm not yet ready to accept the apology.
The performance of an algorithm (also called a policy) is defined as the value of the final prize, minus the sum of all inspection costs. So if we define two indicator random variables:
- $I_i = 1$ if box $i$ is ever opened, $0$ otherwise.
- $A_i = 1$ if prize $i$ is selected, $0$ otherwise.
One might expect this problem to be computationally difficult. The optimal policy must specify the first box to open; then conditioned on any possible prize value found inside, which box to open next; and so on. A priori, there is no reason to expect to be able to even write down such a policy concisely.
Miraculously, however, there is (as Weitzman showed) a simple "index-based" optimal policy. This can actually be viewed as a special case of the independently-discovered Gittins index theorem. Here I describe a proof, with an associated "investment" story, from my paper with Bobby Kleinberg and Glen Weyl.
The proof
Let me actually start by just giving you the optimal policy and proof, to keep it short and contained. Then we'll tell a story that gives the proof more substance.
For each box $i$, split the value $v_i$ into two parts: a capped value and a bonus. Given a "cap" $\sigma_i$ (chosen next), we let $v_i = \kappa_i + b_i$ where
- if $v_i \gt \sigma_i$, then the capped value $\kappa_i = \sigma_i$ and the bonus $b_i = v_i - \sigma_i$.
- if $v_i \leq \sigma_i$, then $\kappa_i = v_i$ and $b_i = 0$ (no bonus).
We say the policy claims above the cap if, whenever box $i$ is opened (that is, $I_i=1$) and the value exceeds its cap (that is, $b_i \gt 0$), box $i$ is selected (that is, $A_i = 1$).
Lemma (Cap Lemma). For any policy, its expected performance is upper-bounded by the expected capped value it obtains: \[ \mathbb{E} \text{performance} \leq \sum_i \mathbb{E} A_i \kappa_i \] with equality if and only if the policy claims above the cap.
Proof. \begin{align} \mathbb{E} \text{performance} &= \sum_i \mathbb{E} \left[A_i v_i - I_i c_i\right] \\ &= \sum_i \mathbb{E} \left[A_i (\kappa_i + b_i) - I_i \mathbb{E} b_i \right] \end{align} by definition of the cap and bonus. Now, the decision to inspect, $I_i$, can only depend on information that is independent of the prize's value (which determines the bonus). So $\mathbb{E} I_i \mathbb{E} b_i = \mathbb{E} I_i b_i$, and rearranging, \begin{align} \mathbb{E} \text{performance} &= \sum_i \mathbb{E} \left[ A_i \kappa_i - (I_i - A_i)b_i \right] \\ &\leq \sum_i \mathbb{E} A_i \kappa_i \end{align} because $b_i \geq 0$ and $A_i \leq I_i$: one can only acquire a prize after opening the box. Furthermore, we have equality iff $(I_i - A_i)b_i = 0$ always, in other words, $b_i \gt 0 \implies A_i = I_i$, i.e. the policy claims above the cap. $\square$
Note the lemma applies to both good and bad policies. For example, the policy that opens no boxes and takes home no prize does satisfy the claim-above-the-cap condition; its expected performance exactly equals the expected capped value it obtains, which is zero.
Corollary. A policy that both claims above the cap and always selects the highest capped value (if any such policy exists) is optimal.
Proof. Since we can only claim one box, the Cap Lemma upper-bounds expected performance by the expected maximum capped value. That is, $\sum_i A_i \leq 1$, so for all policies, \[ \mathbb{E} \text{performance} \leq \sum_i \mathbb{E} A_i \kappa_i \leq \mathbb{E} \max_i \kappa_i. \] If a policy always chooses the item with the highest capped value and it claims above the cap, then the Cap Lemma says it attains this upper bound. $\square$
Corollary. The following policy is optimal: Open the boxes in order of caps $\sigma_i$ from highest to lowest, stopping when the largest observed value $v_{i^*}$ exceeds the highest remaining cap and selecting $i^*$.
Proof. Let us re-word the algorithm as follows: We start a global "clock" counting down from $+\infty$. When the descending clock reaches any $\sigma_i$, we open box $i$ and replace $\sigma_i$ with the capped value $\kappa_i = \min\{v_i, \sigma_i\}$. Once the clock hits some $\kappa_i$, we stop and take prize $i$.
This policy always selects the largest capped value: When the clock reaches $\kappa_i$ and we select it, every other value of $\kappa_j$ (opened boxes) or $\sigma_k$ (unopened boxes) is below $\kappa_i$, and we know that $\kappa_k \leq \sigma_k$ by definition.
It also claims above the cap: if $v_i \geq \sigma_i$, and the clock reaches $\sigma_i$ and we inspect, then we will set $\kappa_i = \sigma_i$ and so we immediately claim prize $i$. $\square$
An investment story
Imagine a generous investor has come with you to Pandora's department store to help you open boxes. The investor is willing to completely subsidize the cost of any box opening, but if the prize in that box exceeds its cap, then you must pay the "bonus" amount to the investor. (This payment is due regardless of whether you claim that prize!)
Now, if you always uphold your end of the bargain, then the investor breaks even on average, by definition of the fair cap: she pays the cost and gets the bonus. \[ c_i = \mathbb{E} b_i .\] So if the investor's average utility is zero, then your utility in this investment-funded world is exactly equal, on average, to your utility in the regular Pandora's box problem.
But what is your utility? You don't pay any costs to open boxes, but you also give up on bonuses. So your utility for getting a prize $v_i$ will be your capped value, $\kappa_i$. However, you might lose some additional money. What if you open a box, see that the prize exceeds its cap, but you don't end up claiming that prize? You must still repay the bonus amount to the investor.
So if we let $i^*$ be the prize you end up claiming, your utility is \[ \kappa_{i^*} - \sum_i (I_i - A_i)b_i \] that is, you get the capped value from the prize you claimed, minus the total amount of bonuses from all prizes that you inspected but did not claim.
Of course, if your policy claims above the cap -- that is, any time you observe a nonzero bonus, you claim the prize -- then the additional repayment is zero, and your utility is equal to $\kappa_{i^*}$.
So we get that your utility is (rewriting to emphasize similarity to the previous section) \begin{align} \text{performance} &= \sum_i \left[ A_i \kappa_i - (I_i-A_i)b_i \right] \\ &\leq \sum_i A_i \kappa_i \end{align} with equality iff you claim above the cap. Remember we said that on average your utility in the investment world is equal to your utility in the original world (because the investor breaks even); so taking an expectation on both sides proves the Cap Lemma. $\square$
However, note that the utilities in the two worlds are not equal for every realization of random values -- just on average. For instance, you may occasionally receive a giant prize $v_{i^*}$ in the original world, but here the investor will scoop up the big bonus and leave you with a capped return.
There is a final subtlety to be discussed. In the original-world proof of the Cap Lemma, we carefully used the assumption that $v_i$ is independent of $I_i$. Here, we have hidden this inside the assumption that the investor breaks even: the amount of investment costs she pays is \[ \sum_i I_i c_i \] while the bonuses she gets back are \[ \sum_i I_i b_i \] and while we have $c_i = \mathbb{E} b_i$, the investor really does expect to break even only if $b_i$ and $I_i$ are independent. If the way I was able to gloss over that worries you, it should! The reliance on the independence assumption is quite tricky and you need to keep an eye on it.
An extension to matching
Here's an extension to a setting that seems much harder, but is not much more work.
Suppose we are matching people $i$ to items $j$ (each wants at most one item). We know that person $i$'s value for item $j$ is drawn from a distribution $D_{ij}$ independently from all others, but it costs $c_{ij}$ to inspect and learn the exact value $v_{ij}$.
Now a policy must inspect the edges $(i,j)$ in some order, matching people to items conditioned on information revealed and items remaining. And as far as we know, the optimal policy may really be hard to compute or require exponential space to write down (proving this is an open problem). Nevertheless, we can do pretty well simply.
For each edge $(i,j)$, we can picture a Pandora box costing $c_{ij}$ to open and with $v_{ij} \sim D_{ij}$. Define the cap $\sigma_{ij}$, bonus $b_{ij}$, and capped value $\kappa_{ij}$ exactly as above. Let $I_{ij} = 1$ if the edge is inspected and $A_{ij} = 1$ if selected in the final matching.
Performance is the sum of realized edges in the matching, minus inspection costs: \[ \text{performance} = \sum_{ij} \left[ A_{ij}v_{ij} - I_{ij}c_{ij} \right] \] with the constraint that $\{A_{ij}\}$ must determine a matching and $I_{ij} \geq A_{ij}$.
Lemma (Cap Lemma, matching setting). For any policy, its expected performance is upper-bounded by total expected capped value, with equality if and only if it claims above the cap: \[ \mathbb{E} \text{performance} \leq \sum_{ij} \mathbb{E} A_{ij} \kappa_{ij} . \]
Proof. Exercise (only syntactic changes from the previous proof).
Given a bipartite graph with edges labeled by capped values $\{\kappa_{ij}\}$, let GREEDY$\{\kappa_{ij}\}$ denote the greedy algorithm's matching: the edge with the largest $\kappa_{ij}$ is matched, and vertices $i$ and $j$ removed along with all their edges; then the next-largest available, and so on.
Corollary. No policy's expected performance exceeds twice the expected value of GREEDY$\{\kappa_{ij}\}$.
Proof. As is well-known, the greedy matching achieves at least half of the optimal max-weighted matching in any bipartite graph. (Proof: The first edge $\kappa_{ij}$ greedily matched is either in OPT, or else rules out at most two edges in OPT incident to $i$ and $j$, each of which is smaller than $\kappa_{ij}$. Repeat.) The Cap Lemma implies that the performance of any policy is upper-bounded by the expected optimal max-weighted matching in this graph, as this maximizes the lemma's upper-bound. $\square$
Corollary. The following policy achieves at least half of the optimal expected performance: Inspect the edges in order of caps $\sigma_{ij}$ from highest to lowest, pausing whenever the largest observed value $v_{ij}$ exceeds the highest remaining cap, matching the edge $(i,j)$, and removing all edges incident to $i$ and $j$ from the graph, then continuing.
Proof. Re-word the algorithm: A global descending clock counts down from $+\infty$; when it reaches any remaining $\sigma_{ij}$ we inspect and replace that edge with its capped value $\kappa_{ij} = \min\{v_{ij},\sigma_{ij}\}$; when the clock reaches any $\kappa_{ij}$, we match that edge and remove its vertices and their incident edges.
This policy implements the greedy matching with respect to capped values: When the clock reaches any $\kappa_{ij}$ and we match that edge, it really is the largest capped value of any of the remaining edges in the graphs, as they all have either smaller capped values $\kappa_{kl}$ (inspected edges) or simply smaller caps $\sigma_{kl}$ (uninspected edges).
Furthermore, this policy claims above the cap, since whenever we inspect an edge and find $b_{ij} \gt 0$, we set $\kappa_{ij} = \sigma_{ij}$ and immediately claim that edge. So by the Cap Lemma, this policy achieves exactly its expected sum of capped values, which equals the greedy matching of capped values; by the above corollary, this is a two-approximation to the optimal policy. $\square$
A cool point here is that the optimal policy does not seem to have any simple form. (Think about optimal algorithms for weighted bipartite matching, what information they require, and how to acquire it without wasted inspection costs!) So this extension, even though it's technically almost no harder to prove, shows how the "cap" formalism can give upper bounds on complex optimal policies.
If you're interested to learn more on combining information-acquisition problems with combinatorial optimization, you're in luck: a paper was written just for you. Check out Singla 2018.
References
(1979) Martin L. Weitzman. Optimal search for the best alternative. Econometrica.(1992) Richard Weber. On the Gittins Index for Multiarmed Bandits. Annals of Applied Probability.
(2016) Robert Kleinberg, Bo Waggoner, and E Glen Weyl. Descending price coordinates approximately efficient search. Proceedings of the 17th ACM Conference on Economics and Computation.
(2018) Sahil Singla. The price of information in combinatorial optimization. Proceedings of the 29th Annual ACM-SIAM Symposium on Discrete Algorithms.