Eliciting Properties of Distributions
Posted: 2017-04-12.
Continuing the series on elicitation, we'll take a look at properties or statistics of distributions: things like the mode, median, or variance. This post will focus on the defining elicitation of properties and showing how the convex characterization of proper scoring rules extends. We'll look at more concrete cases and implications in later posts.
What is Truth?
Lambert, Pennock, and Shoham (2008) formalized the setting like this. We will ask a question about a future event $Y$ to some presumed "expert" (actually: golden retriever behind a keyboard somewhere). We will score them with a function $S(r,y)$ when they report $r$ and the outcome is $y$. The key assumption is that the expert wants to maximize her expected score.
You might think that the first question is what scoring rule $S$ to use. But the first question is really: What do we even want them to report in an ideal world?
LPS08 proposed a nice formalization: a property $\Gamma$ which simply defines, for each possible belief of the expert, a set of "correct" reports for someone with that belief. For example, suppose you're Buddy the Expert Dog and your belief is that there is an equal probability that $Y$ is 1, 2, 3, or 4. If the property is the median, then anything in $[2,3]$ is a valid answer. Anything else is not a valid answer.
Formally, we write $\Gamma: \Delta_{\mathcal{Y}} \to 2^{\mathcal{R}}$. Here the outcome space $\mathcal{Y}$ is the set of possible outcomes of the random variable $Y$, and the report space is $\mathcal{R}$, e.g. the real numbers in the median example. $\Gamma(p)$ is the set of "correct" or "allowed" answers for belief $p$. We'll assume non-redundancy in that no two reports are interchangeable (meaning always either both are correct or neither is).
In some cases, we want to restrict to single-valued properties, those where there is only one correct answer for each belief. For instance, the mean is single-valued, but the mode is not (for a fair coin flip, both 0 and 1 are modes of the distribution). In the single-valued case, it's convenient to abuse notation and treat $\Gamma$ as a function from $\Delta_{\mathcal{Y}}$ to $\mathcal{R}$.
Definition. $\Gamma: \Delta_{\mathcal{Y}} \to 2^{\mathcal{R}}$ is (directly) elicitable if there exists a scoring rule $S: \mathcal{R} \times \mathcal{Y} \to \mathbb{R}$ that elicits it, i.e. $$ \Gamma(p) = \arg\max_{r\in\mathcal{R}} ~ \mathbb{E}_p S(r, Y) . $$
I will explain why we're using the term "directly" in, eh, some future blog post.
Definition. A level set of a property $\Gamma$ at a report $r$ is the set of beliefs mapping to that report, i.e. $\{p : r \in \Gamma(p)\}$.
That term comes up pretty often, so it's worth introducing immediately.
Basic (Counter) Examples
The simplest examples are proper scoring rules, where the goal is to elicit the distribution itself: $\Gamma(p) = p$. Other cases, when $p$ is a distribution on the real numbers, are the mean: $\Gamma(p) = \mathbb{E}_p Y$; and the median: $\Gamma(p) = \{r : \Pr[Y \geq r] \geq 0.5 \text{ and } \Pr[Y \leq r] \geq 0.5\}$.
Exercise 1.
Show that the median is elicited by $S(r,y) = -|r-y|$, and the mean by $S(r,y) = -(r-y)^2$.
Hint: use calculus to find the optimal report for a given belief.
Another is the variance. Intuitively, it should not be elicitable without further information. The expert says the random variable has high variance, and the observed outcome is $42$; was she right or wrong? In principle, the distribution could be a point mass at $42$ or it could follow a power law or anything else.
To prove that the variance is not elicitable, we can simply consider a biased coin flip, i.e. distributions on {0,1}. Imagine we have a scoring rule that purports (that's a word) to elicit the variance.
- For a distribution with all its probability mass on "1", the report maximizing expected score must be $0$ because this distribution has zero variance.
- Similarly, if all the probability mass is on "0", then the best report must be $0$ as well.
This idea generalizes to a simple yet extremely general and powerful necessary condition for elicitation:
Theorem 1. If $\Gamma$ is directly elicitable, then its level sets must be convex, i.e. for all $r$, the set $\{p : r \in \Gamma(p)\}$ is a convex subset of $\Delta_{\mathcal{Y}}$.
Exercise 2: Prove it!
Hint 1: See the proof of impossibility for the variance, above.
Hint 2: Suppose that $\Gamma(p) = \Gamma(p') = r$ and consider the implications for reports on the line between $p$ and $p'$.
Of course, this doesn't imply that it's impossible to discover the variance from an expert in some more sophisticated, truthful way. For example, one could use a proper scoring rule to elicit the distribution, then compute the variance. But it does mean there is no, ahem, direct way, i.e. there does not exist an $S$ so that $Var(p) = \arg\max_r \mathbb{E}_p S(r, Y)$.
Technicalities
There are a few technical subtleties worth mentioning. One is that we might sometimes want to allow $S(r,y) = -\infty$. This actually happens in the common log scoring rule $S(p,y) = \log p(y)$. If someone predicts e.g. that there is a zero probability that a certain tiny-handed blonde gets elected president, but that "impossible" event actually happens, then the score is $\log 0 = -\infty$. The interpretation of $-\infty$ here is that the agent is punished with some extreme worst-imaginable punishment, such as having her head cut off or actually having said blonde as president.
One way to avoid doing math with inifity (although it's not a problem and is common, even crucial in convex analysis) is to restrict the space of beliefs to some $\mathcal{P}$, such as all distributions with full support.
But this kind of restriction will be useful in other scenarios too. Suppose $Y$ is distributed on the entire real line, and we want to elicit the agent's expectation. Well, it would be extremely helpful if this expectation were to exist, for example, the agent's belief $p$ does not follow a Cauchy distribution or similar. So we'd restrict $\mathcal{P}$ to be the space of measures on the real line with finite expectation. (Speaking of measure - I'm going to take some technical liberties below by using notation that works fine in the finite-outcome case, but needs some (missing) development in more general settings. You've been warned.)
General Characterization
The key point, just as with proper scoring rules, is the connection to convex functions. This point doesn't quite appear in any one paper as far as I'm aware, but it's basically inferable (that's a word) from the literature: mainly Frongillo and Kash 2014, building on the combination of proper scoring rule papers (e.g. Gneiting and Raftery 2007) and property elicitation papers (e.g. Lambert et al. 2008, Lambert and Shoham 2009).
It's ok for this to not make much sense or seem very interesting until you've seen some pictures and examples. We're starting in the greatest generality here so that later, interesting special cases will make sense as part of the same general framework. But it may take seeing those examples and pictures in order to internalize this characterization, and that's fine.
Theorem 2. Suppose that $\Gamma: \mathcal{P} \to 2^{\mathcal{R}}$ is elicitable, by some $S(r,y)$. Let $S(r;\cdot)$ be the affine function $S(r;q) := \mathbb{E}_q S(r,Y)$. Then there exists a convex function $G: \mathcal{P} \to \mathbb{R}$ such that:
- $G(p)$ is the expected score for making any truthful report with belief $p$.
- For each report $r$, the function $S(r;\cdot)$ is a subtangent of $G$, i.e. can be written $S(r;q) = G(p) + d(r) \cdot (q-p)$ for some $p$ with $r \in \Gamma(p)$ and $d(r)$ a subgradient of $G$ at $p$.
- Furthermore $S(r;\cdot)$ is tangent at exactly the level set of $r$, i.e. the set of beliefs for which $r$ is truthful.
Recall that a subtangent is an affine function that lies weakly below $G$ and equals $G$ at some point.
This theorem might sound pretty technical, but there are good geometric reasons for what's going on. Hopefully it sounds familiar from proper scoring rules and their characterization proof; if not, take a look. We'll also draw a few pictures later on.
Proof of theorem. Suppose $\Gamma$ is elicited by $S$. Define the function $G(p) := S(\Gamma(p);p)$ by choosing any $r \in \Gamma(p)$ to plug in. To see that this is well-defined, notice that if $r,r'$ are both acceptable reports for belief $p$, then their expected scores must be equal under belief $p$; otherwise, $S$ would only elicit the one with higher expected score. Of course, by definition $G(p)$ is the expected score for truthfully reporting some $r \in \Gamma(p)$.
$G$ is convex because each $S(r;\cdot)$ is an affine function (it is an expectation) and $G$ is the pointwise maximum of these functions, i.e. $G(p) = \max_r S(r;p)$ (this follows from truthfulness, that $r$ maximizes expected score for $p$). This implies that $S(r;\cdot)$ lies entirely below $G$ and is tangent at $p$ for any $p$ with $r \in \Gamma(p)$. So $S(r;\cdot)$ is a subtangent of $G$ at all such $p$. Finally, it is a subtangent at only such $p$: If $r \not\in \Gamma(p)$, then $S(r;p) \neq \max_{r'} S(r';p) = G(p)$.
The converse is true as well: Given any convex function, we get an elicitable property.
Theorem 3. Let $G: \mathcal{P} \to \mathbb{R}$ be convex. Then $\Gamma(p) = \{ d : d \text{ is a subgradient of } G \text{ at } p \}$ is an elicitable property, and moreover is elicited by $S(d,y) := G(p) + d \cdot (\delta_y - p)$ where $p$ is chosen arbitrarily subject to $d \in \Gamma(p)$.
Proof. We just need to show that $S$ elicits $\Gamma$. The expected score for report $d$ under belief $q$ is $S(d;q) = G(p) + d \cdot (q - p)$ for some $p$ with $d \in \partial G(p)$, that is, $d$ a subgradient at $p$. By definition of a subgradient at $p$, this gives $S(d;q) \leq G(q)$. So the maximum possible expected score for belief $q$ is $G(q)$. To finish the proof, I claim that $S(d;q) = G(q)$ if and only if $d$ is a subgradient at $q$, QED.
Exercise 3: Prove my claim: Show that if $d$ is a subgradient of $G$ at $p$, and $G(p) + d \cdot (q-p) = G(q)$, then $d$ is a subgradient of $G$ at $q$.
Hint: Use the definition of subgradient directly.
There is a slight brain-twister in Theorem 3: The "name" of each property value in $\Gamma(p)$ is a subgradient of $G$ at $p$. Who cares about properties of this form? The key point to remember is that we could "relabel" or rename these and get essentially the same property. For example, consider the property $\Gamma(p) = p$, or the property $\Gamma(p) = 1000p$. They have the same level sets, so they're identical from an elicitation point of view. The names we give to properties don't matter for elicitability.
There is an interesting extension to Theorem 3. Notice that in elicitation, each belief only has to have at least one "correct" report. But it doesn't have to have more than one. If $G$ has many subgradients at $p$, it is not necessary that all of them be reports; one could also consider a smaller property $\Gamma'$ whose space of possible reports simply omits some of these excess subgradients at $p$.
Examples
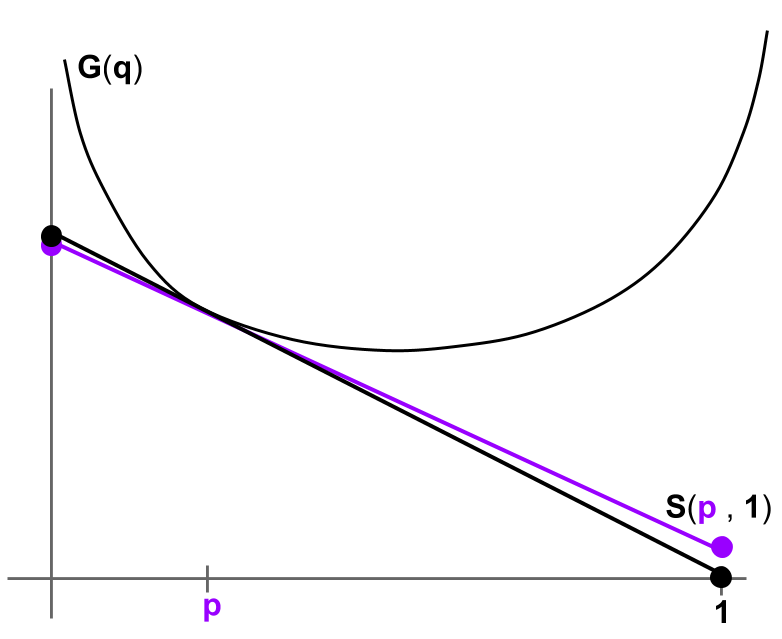
Illustration for a proper scoring rule eliciting a distribution $p$ on two outcomes, heads and tails. The horizontal axis is the probability of heads. The property is $\Gamma(p) = p$. Note that technically, $p$ is a two-dimensional vector (a point in the simplex on two outcomes). However, $G$ is only defined on the simplex, i.e. the line between the points $(0,1)$ and $(1,0)$. So we abuse the math a bit by drawing $p$ as a scalar in $[0,1]$ and drawing $G$ above the interval.
Each report corresponds to a different subgradient. Here, strict convexity gives that even a small change in $p$ results in a different tangent line slope (the difference between the purple and black tangents), hence a different optimal report.
For example, this could be a badly-drawn graph of $G(p) = p^2 + (1-p)^2$, which gives a form of the quadratic scoring rule.
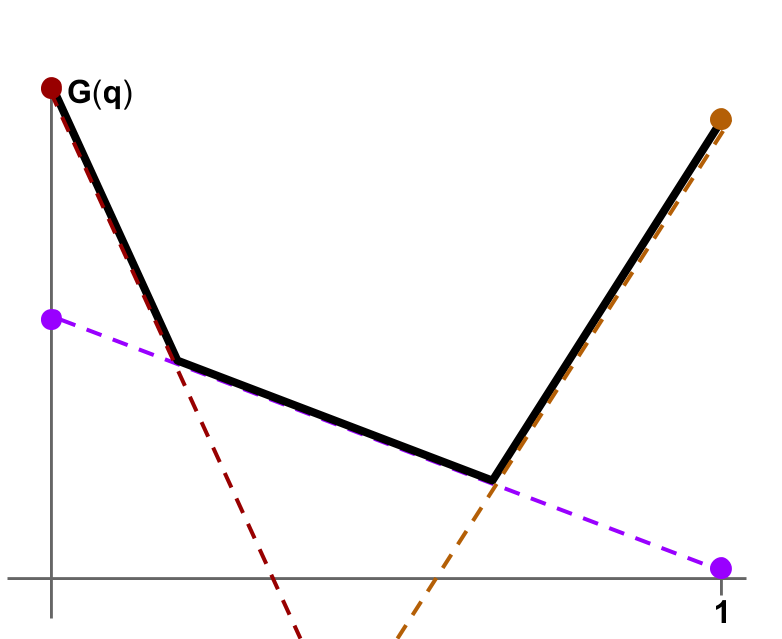
Here $\Gamma(p)$ has three possibilities: (A) $p \leq 0.2$; (B) $0.2 \leq p \leq 0.6$; (C) $0.6 \leq p$. These three reports each have an associated subgradient (the slopes of the three different dotted lines): A is the leftmost red one; B the middle, purple; C the rightmost orange. $\Gamma$ is not single-valued; at $p=0.2$ and $p=0.6$, there are two "correct" reports.
Here $G$ is (let's say) $G(p) = 1-3p$ for $p \leq 0.2$, $G(p) = 0.5 - 0.5p$ for $0.2 \leq p \leq 0.6$; and $G(p) = -1 + 2p$ for $0.6 \leq p$. $S$ can be read off from the endpoints of the respective subtangent lines, for example, $S(A,\cdot)$ is given by the endpoints of the leftmost red dotted line. So $S(A,\text{tails}) = 1$, $S(A,\text{heads}) = -2$, $S(B,\text{tails}) = 0.5$, $S(B, \text{heads}) = 0$, $S(C, \text{tails}) = -1$, and $S(C, \text{heads}) = 1$.
The expected score for a given report (say $B$) under a given belief (say $q=0.1$) is given by the value of the subtangent dotted line at that belief, in this case the purple line at $0.1$ has height $0.4$. A report is truthful for a belief if and only if the subtangent line actually touches $G$ at that belief.
Let's leave more details for later posts, where we can look in depth at interesting cases like finite properties (the range of $\Gamma$ is a finite set), properties where $\Gamma$ is a continuous function into the reals, and others.
Exercise 4.
Show that the following property is elicitable for distributions on two outcomes: $\Gamma(p) = A$ if $p \leq 0.5$, $\Gamma(p) = B$ if $p \geq 0.5$.
(Note this is sloppy notation: I really mean $\Gamma(p) = \{A\}$ if $p \lt 0.5$, $\{B\}$ if $p \gt 0.5$, and $\{A,B\}$ if $p = 0.5$.)
Draw a convex expected score function $G$ associated with a scoring rule that elicits it.
Exercise 5.
Show that the following property is not elicitable: $A \in \Gamma(p)$ iff $p \leq 0.3$ or $p \geq 0.7$; $B \in \Gamma(p)$ iff $0.3 \leq p \leq 0.7$.
Here the report A corresponds to "the distribution is relatively biased" while B corresponds to "the distribution is relatively unbiased".
Problem 1.
Describe as broad as possible a class of scoring rules that elicit the median.
Hint: what if we first add $2$ to both the report and the outcome? What else can we do?
References
(2007) Tilman Gneiting and Adrian E. Raftery. Strictly proper scoring rules, prediction, and estimation. Journal of the American Statistical Association.(2008) Nicolas S Lambert, David M Pennock, and Yoav Shoham. Eliciting properties of probability distributions. Proceedings of the 9th ACM Conference on Electronic Commerce.
(2009) Nicolas Lambert and Yoav Shoham. Eliciting truthful answers to multiple-choice questions. Proceedings of the 10th ACM Conference on Electronic Commerce.
(2014) Rafael Frongillo and Ian Kash. General truthfulness characterizations via convex analysis. Proceedings of the 10th Conference on Web and Internet Economics.

